
Chi Square Membongkar Masalah Filling 650ml, Chi-square merupakan alat statistik yang sangat berguna dalam konteks Lean Six Sigma. Dalam upaya meningkatkan kualitas dan efisiensi proses bisnis, Lean Six Sigma memerlukan analisis data yang mendalam untuk mengidentifikasi faktor-faktor yang mempengaruhi keberhasilan atau kegagalan suatu proses. Dalam hal ini, Chi-square dapat digunakan untuk menganalisis hubungan antara variabel-variabel yang terlibat dalam proses tersebut. Dengan memahami hubungan ini, kita dapat mengidentifikasi penyebab utama ketidaksempurnaan dalam proses dan mengambil langkah-langkah perbaikan yang tepat. Dengan menggunakan Chi-square sebagai alat analisis, kita dapat mendorong pemahaman yang lebih baik tentang faktor-faktor yang mempengaruhi kualitas dan efisiensi proses, sehingga membantu dalam penyelesaian masalah Lean Six Sigma yang lebih efektif.
Uji Chi Square
Dalam perjalanan yang mendalam untuk meningkatkan kualitas dan efisiensi suatu proses melalui pendekatan Lean Six Sigma, seorang praktisi harus cermat dalam menganalisis hubungan antara variabel-variabel yang terlibat. Salah satu instrumen yang amat berharga dalam analisis ini adalah uji chi-square.
Mari kita berhenti sejenak dan merenung tentang bagaimana uji ini dapat bermanfaat. Misalnya, bayangkan seorang analis yang ingin meneliti hubungan antara volume filling botol 650ml (variabel X) dan tingkat kepuasan konsumen (variabel Y). Dalam situasi ini, uji chi-square bisa menjadi alat yang sangat berguna untuk menjelajah lebih dalam.
Pertama-tama, analis harus membuat tabel kontingensi. Tabel ini sangat penting karena ia menggambarkan frekuensi pengamatan pada setiap kombinasi nilai dari variabel X dan Y. Dengan tabel ini sebagai dasar, analis dapat menghitung nilai chi-square. Selanjutnya, nilai ini perlu dibandingkan dengan nilai kritis yang sesuai, yang telah ditentukan berdasarkan tingkat signifikansi yang dipilih.
Jika analis menemukan bahwa nilai chi-square yang dihitung melebihi nilai kritis, maka kesimpulan yang dapat ditarik adalah bahwa terdapat hubungan yang signifikan antara kedua variabel tersebut. Namun, jika nilai chi-square tidak melebihi nilai kritis, maka tidak dapat dikatakan ada hubungan yang signifikan antara kedua variabel tersebut.
Jadi, penting bagi analis untuk memahami dan menggunakan uji chi-square ini dengan hati-hati. Dengan menggali lebih dalam melalui analisis ini, kita dapat memperoleh pemahaman yang lebih baik tentang hubungan antara volume filling botol 650ml dan tingkat kepuasan konsumen. Semoga ini dapat membantu dalam pengambilan keputusan yang lebih baik dan perbaikan yang lebih efektif dalam menghadapi tantangan di dunia bisnis.
Dalam kerangka kerja Lean Six Sigma, pemanfaatan uji chi-square ini memiliki implikasi yang mendalam. Hal ini memungkinkan analis untuk mengidentifikasi faktor-faktor yang berpotensi memiliki kontribusi signifikan terhadap tantangan yang dihadapi dalam proses yang sedang dianalisis. Dengan wawasan yang lebih mendalam tentang hubungan antara variabel-variabel ini, strategi perbaikan yang lebih efektif dapat dirancang dan tindakan yang tepat dapat diambil untuk mengoptimalkan kualitas dan efisiensi proses.
Lebih jauh, dalam mengadopsi pendekatan hipotesis statistik, penting untuk memahami peran dari Ho dan Ha. Ho, atau hipotesis nol, menyatakan bahwa tidak ada perbedaan atau hubungan yang signifikan antara dua variabel atau fenomena yang sedang diuji. Sebagai titik awal, ini adalah asumsi yang meragukan adanya efek atau perubahan.
Sementara itu, Ha, atau hipotesis alternatif, menawarkan pandangan yang berbeda. Ha menyatakan bahwa ada perbedaan atau hubungan yang signifikan antara variabel atau fenomena yang sedang diuji. Ini menantang Ho dan mengusulkan alternatif.
Dalam melakukan analisis hipotesis statistik, sangatlah penting untuk merumuskan Ho dan Ha dengan jelas, dan kemudian menggunakan data yang relevan untuk melakukan pengujian statistik. Hasil dari pengujian ini akan menjadi pencerah dalam menentukan apakah ada bukti yang cukup untuk menolak Ho dan mendukung Ha.
Penguasaan yang mendalam tentang Ho dan Ha sangat penting, karena hasil pengujian statistik akan memberikan informasi berharga yang akan membantu dalam pembuatan keputusan yang berlandaskan bukti.
Sebagai kesimpulan, uji chi-square dan pemahaman yang baik tentang penggunaan hipotesis dalam analisis statistik adalah aset berharga dalam perjalanan untuk mencapai peningkatan kualitas dan efisiensi melalui pendekatan Lean Six Sigma.
Bedah Kasus Volume Botol 650ml
Dalam lingkungan yang dinamis seperti industri Fast-Moving Consumer Goods (FMCG), pemahaman mendalam mengenai kualitas produk adalah aspek krusial. Perusahaan yang bergerak dalam bidang ini sering kali berhadapan dengan tantangan untuk memastikan bahwa produk mereka memenuhi standar yang telah ditetapkan. Salah satu contoh klasik adalah dalam kasus perusahaan FMCG yang memproduksi minuman dalam botol 65ml.
Bayangkan, sebagai bagian dari tim kontrol kualitas, Anda memiliki tanggung jawab untuk memastikan bahwa volume minuman dalam setiap botol adalah 65ml. Dalam situasi ini, uji chi-square dan analisis hipotesis dapat menjadi alat yang sangat berharga.
Misalkan, Anda ingin mengetahui apakah ada hubungan antara hari produksi (misalnya, Senin, Selasa, …, Minggu) dan frekuensi botol yang tidak memenuhi kriteria volume 65ml. Dalam hal ini, variabel hari produksi adalah variabel kategorikal X dan variabel frekuensi ketidaksesuaian volume adalah variabel kategorikal Y.
Sebelum memulai analisis, penting untuk merumuskan hipotesis. Hipotesis nol (Ho) dalam kasus ini mungkin menyatakan bahwa tidak ada hubungan antara hari produksi dan frekuensi ketidaksesuaian volume minuman dalam botol. Sementara itu, hipotesis alternatif (Ha) menyatakan bahwa ada hubungan yang signifikan antara kedua variabel tersebut.
Setelah merumuskan hipotesis, langkah selanjutnya adalah mengumpulkan data. Misalnya, selama beberapa minggu, Anda mencatat jumlah botol yang tidak memenuhi kriteria volume 65ml untuk setiap hari produksi.
Dengan data ini, Anda dapat membuat tabel kontingensi yang menggambarkan frekuensi pengamatan pada setiap kombinasi hari produksi dan frekuensi ketidaksesuaian volume. Kemudian, nilai chi-square dihitung berdasarkan tabel ini.
Dengan membandingkan nilai chi-square yang dihitung dengan nilai kritis yang sesuai dengan tingkat signifikansi yang ditentukan (misalnya, 0.05), Anda dapat menentukan apakah harus menolak hipotesis nol.
Jika nilai chi-square melebihi nilai kritis, ini menunjukkan bahwa ada hubungan yang signifikan antara hari produksi dan frekuensi ketidaksesuaian volume, sehingga menolak Ho dan mendukung Ha. Dalam konteks ini, temuan ini dapat membantu perusahaan dalam mengidentifikasi hari-hari tertentu yang mungkin memerlukan perbaikan dalam proses produksi.
Sebaliknya, jika nilai chi-square tidak melebihi nilai kritis, maka tidak ada bukti yang cukup untuk menolak Ho, dan dapat disimpulkan bahwa tidak ada hubungan yang signifikan antara hari produksi dan frekuensi ketidaksesuaian volume.
Penting untuk dicatat bahwa uji chi-square dan analisis hipotesis adalah alat yang sangat berharga dalam mengevaluasi dan meningkatkan kualitas produk dalam industri FMCG. Dengan memanfaatkan metode ini dengan cermat, perusahaan dapat mengambil langkah-langkah tepat untuk mengoptimalkan proses produksi dan memastikan kepuasan pelanggan.
Misalkan sebuah perusahaan FMCG ingin mengevaluasi apakah ada hubungan antara hari produksi dan ketidaksesuaian volume minuman dalam botol 65ml.
Data yang dikumpulkan selama dua minggu adalah sebagai berikut:
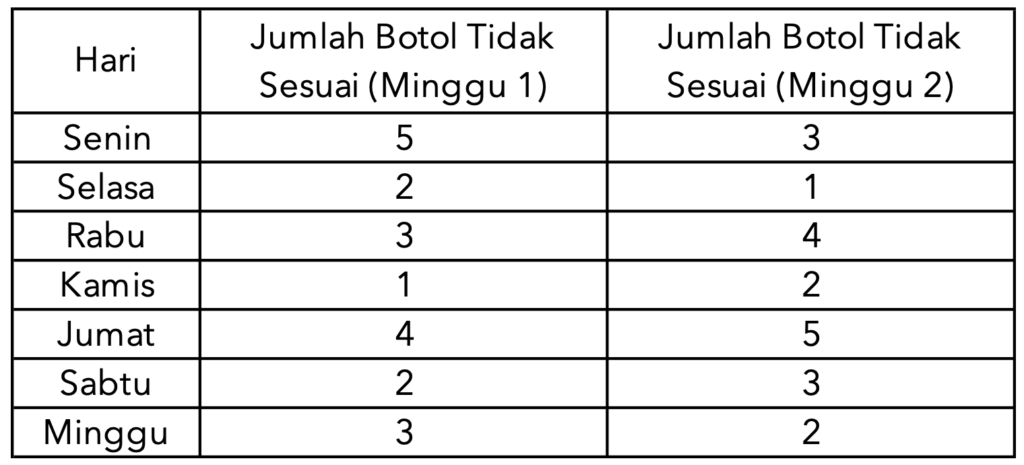
Pertama, mari kita rumuskan hipotesis:
- Ho: Tidak ada hubungan antara hari produksi dan ketidaksesuaian volume minuman dalam botol.
- Ha: Ada hubungan yang signifikan antara hari produksi dan ketidaksesuaian volume minuman dalam botol.
Tahapan Pemecahan Masalah Chi Square
Langkah-langkah dalam menghitung uji Chi Square (X²).
Langkah 1: Siapkan Tabel Data
Pertama, Anda harus memiliki tabel data yang berisi frekuensi observasi. Dalam kasus ini, tabel yang diberikan adalah sebagai berikut:

Langkah 2: Hitung Nilai Ekspektasi
Nilai ekspektasi adalah nilai yang diharapkan dalam setiap sel tabel jika tidak ada keterkaitan antara dua variabel. Ini dihitung dengan rumus:
E = (Total baris * Total kolom) / Total keseluruhan
Sebagai contoh:
Untuk Senin, A: E = (820)/40 = 4
Untuk Senin, B: E = (820)/40 = 4
Untuk Selasa, A: E = (320)/40 = 1.5
Untuk Selasa, B: E = (320)/40 = 1.5
Untuk Rabu, A: E = (720)/40 = 3.5
Untuk Rabu, B: E = (720)/40 = 3.5
… dan seterusnya.

Langkah 3: Hitung Selisih Kuadrat antara Observasi dan Ekspektasi dibagi dengan Ekspektasi
Rumusnya adalah ((O – E)²) / E untuk setiap sel.
Sebagai contoh, untuk Senin pada kolom A, ((5-4)²)/4 = 0.25.

Langkah 4: Hitung Nilai Chi Square (X²)
Penjumlahan semua nilai yang dihitung pada langkah 3.
X² = Σ[((O – E)²) / E]
= 0.25 + 0.25 + 0.17 + 0.17 + 0.07 + 0.07 + 0.17 + 0.17 + 0.06 + 0.06 + 0.1 + 0.1
= 1.206
Langkah 5: Bandingkan dengan Nilai Kritis Chi Square
Untuk menentukan apakah ada keterkaitan yang signifikan antara dua variabel, bandingkan nilai X² yang Anda dapatkan dengan nilai kritis dari tabel Chi Square pada tingkat kepercayaan yang Anda pilih (misalnya, 0.05) dengan derajat kebebasan yang sesuai.
Nilai ini akan digunakan untuk menentukan Derajat kebebasan (df), apakah ada keterkaitan yang signifikan antara variabel di tabel. Anda bisa membandingkannya dengan nilai tabel Chi Square pada tingkat kepercayaan tertentu (misalnya 0.05) dengan derajat kebebasan (jumlah baris-1) * (jumlah kolom-1) = (7-1)*(2-1) = 6.
Jika nilai X² yang dihitung lebih besar dari nilai kritis, maka kita dapat menyimpulkan bahwa ada keterkaitan yang signifikan antara dua variabel. Jika lebih kecil, maka kita tidak dapat menyimpulkan adanya keterkaitan yang signifikan.
Menggunakan perangkat lunak statistik atau kalkulator chi-square, kita mendapatkan nilai chi-square sebesar 1.206 dengan 6 derajat kebebasan. Berapa Nilai kritis chi-square untuk 6 derajat kebebasan dan tingkat signifikansi 0.05 adalah sekitar 12.59.

Dalam hal ini, karena nilai chi-square yang dihitung (2.6) kurang dari nilai kritis (12.59), kita tidak memiliki cukup bukti untuk menolak hipotesis nol. Ini berarti bahwa, berdasarkan data yang kita miliki, tidak ada hubungan yang signifikan antara hari produksi dan ketidaksesuaian volume minuman dalam botol.
Penting untuk menginterpretasikan hasil ini dengan kehati-hatian. Ini tidak berarti bahwa tidak ada faktor lain yang mungkin mempengaruhi ketidaksesuaian volume; hanya menunjukkan bahwa, berdasarkan data yang kita analisis, kita tidak dapat menyimpulkan bahwa hari produksi adalah faktor yang signifikan. Sebagai tim kontrol kualitas, penting untuk terus memantau proses dan mungkin mempertimbangkan variabel lain yang dapat mempengaruhi kualitas produk.
Selamat mencoba! Salam Produktivitas!
Dan Anda bisa terus belajar bersama dengan kami di Jago Kaizen dan Coach Wawang.
Ingin mempelajari secara langsung dan privat tentang LEAN Six Sigma?
Atau Anda ingin mengundang, trainer dan consulting provider?
PT Mitra Prima Produktivitas adalah provider coaching, mentoring, training, dan consulting ternama di Indonesia untuk kinerja Produktivitas dan peningkatan Profitabilitas.




