
Baik, Sahabat Pembaca! Bertemu lagi kita. Senang sekali rasanya.
Kali ini kita akan membahas tentang Cara Pintar Implementasi Six Sigma dengan Teknik Statistik yaitu penggunaan alat statistik dalam metodologi Six Sigma. Dalam proses analisis dan pengendalian kualitas, Six Sigma seringkali menggunakan berbagai alat statistik untuk membantu mengidentifikasi penyebab variasi dalam proses produksi atau layanan.
Istilah Penting Teknik Statistic dalam Aplikasi Six Sigma
Berikut ini adalah beberapa istilah penting yang perlu kita ketahui:
- Data. Data adalah informasi yang dihasilkan dari pengukuran, observasi, atau pengumpulan informasi. Dalam konteks Six Sigma, data digunakan untuk menggambarkan proses yang sedang dianalisis dan membantu mengidentifikasi area yang memerlukan perbaikan. Contoh: jumlah produk cacat dalam satu hari, waktu siklus produksi, atau biaya produksi.
- Populasi. Populasi adalah keseluruhan elemen atau anggota dari suatu kelompok yang sedang dianalisis. Dalam konteks Six Sigma, populasi bisa berupa semua produk yang dihasilkan perusahaan dalam satu tahun, atau seluruh transaksi yang dilakukan di suatu bank dalam satu bulan.
- Sampel. Sampel adalah sekelompok elemen yang dipilih dari populasi untuk dianalisis. Dalam Six Sigma, pengambilan sampel digunakan untuk mengurangi waktu dan biaya pengumpulan data, serta memberikan informasi yang akurat tentang karakteristik populasi. Contoh: mengambil sampel 100 produk dari total 10.000 produk yang dihasilkan perusahaan dalam satu tahun.
- Varians. Varians adalah ukuran seberapa jauh nilai-nilai dalam suatu kumpulan data bervariasi dari rata-rata. Dalam Six Sigma, varian digunakan untuk mengukur variasi dalam proses produksi atau layanan. Semakin rendah varian, semakin konsisten proses tersebut. Contoh: menghitung varian waktu siklus produksi untuk menilai konsistensi proses.
- Deviasi. Deviasi adalah perbedaan antara nilai observasi dan rata-rata. Dalam konteks Six Sigma, deviasi digunakan untuk mengidentifikasi titik data yang jauh dari rata-rata, yang mungkin menunjukkan adanya masalah dalam proses. Contoh: mengidentifikasi produk dengan waktu siklus produksi yang jauh lebih lama dari rata-rata.
- Hipotesis. Hipotesis adalah pernyataan yang diajukan untuk diuji kebenarannya melalui pengumpulan dan analisis data. Dalam Six Sigma, pengujian hipotesis digunakan untuk menentukan apakah perubahan yang diusulkan dalam proses akan menghasilkan perbaikan yang signifikan. Contoh: menguji hipotesis bahwa mengurangi jumlah langkah dalam proses produksi akan mengurangi jumlah produk cacat.
Hypothesis dalam Aplikasi Statistic Six Sigma
Sahabat Pembaca!
Hipotesis tidak lepas dari yang Namanya Pvalue dan angka tingkat kepercayaan (confidence level).
Nilai P atau Pvalue adalah suatu nilai yang digunakan dalam statistik inferensial untuk mengukur seberapa signifikan hasil pengujian hipotesis. Nilai P merupakan probabilitas mendapatkan hasil yang sama atau lebih ekstrem dari yang diamati, jika hipotesis nol benar. Jadi, nilai P memberikan gambaran seberapa kuat bukti melawan hipotesis nol. Semakin kecil nilai P, semakin kuat bukti yang menolak hipotesis nol.
Dalam pengujian hipotesis, kita membandingkan nilai P dengan tingkat signifikansi (α) yang telah ditentukan sebelumnya (biasanya 0,05 atau 5%). Jika nilai P lebih kecil dari α, maka kita menolak hipotesis nol dan menerima hipotesis alternatif. Sebaliknya, jika nilai P lebih besar dari α, kita gagal menolak hipotesis nol.
“Raih kesuksesan dalam bisnismu dengan menerapkan Lean Six Sigma bersama PT Mitra Prima Produktivitas dan Coach Wawang yang difasilitasi oleh pembicara dan konsultan senior berlisensi internasional. Daftar sekarang untuk memulai perjalananmu!”
Contoh praktis: Misalkan kita ingin menguji apakah pelatihan baru yang diberikan kepada karyawan perusahaan mampu meningkatkan produktivitas mereka. Kita tentukan tingkat kepercayaan (confidence level) sebesar 95%, sehingga tingkat signifikansi (α) adalah 0,05. Setelah mengumpulkan dan menganalisis data, kita mendapatkan nilai P sebesar 0,03.
Karena nilai P (0,03) lebih kecil dari α (0,05), kita menolak hipotesis nol (pelatihan baru tidak memiliki pengaruh terhadap produktivitas karyawan) dan menerima hipotesis alternatif (pelatihan baru meningkatkan produktivitas karyawan). Dalam hal ini, kita memiliki bukti yang cukup kuat untuk menyatakan bahwa pelatihan baru efektif dalam meningkatkan produktivitas karyawan.
Jadi, nilai P sangat berguna dalam membantu kita mengambil keputusan berdasarkan hasil pengujian hipotesis, dengan mempertimbangkan tingkat kepercayaan dan risiko yang telah ditetapkan. Semoga penjelasan ini membantu Anda memahami konsep nilai P dan penerapannya dalam praktik.
Sahabat Pembaca!
Sekarang mari kita bahas mengenai hipotesis, hipotesis nol, hipotesis alternatif, serta angka keyakinan (confidence value) dan kaitannya dengan nilai alpha dan beta.
Hipotesis adalah pernyataan yang diajukan untuk diuji kebenarannya melalui pengumpulan dan analisis data. Hipotesis membantu kita membuat asumsi tentang suatu hubungan atau karakteristik yang kemudian akan diuji menggunakan metode statistik.
- Hipotesis Nol (H₀). Hipotesis nol adalah pernyataan yang mengasumsikan tidak ada perbedaan atau hubungan antara variabel yang sedang dianalisis. Dalam pengujian hipotesis, tujuannya adalah untuk menguji apakah bukti yang ada cukup kuat untuk menolak hipotesis nol.
- Hipotesis Alternatif (H₁). Hipotesis alternatif adalah pernyataan yang bertentangan dengan hipotesis nol. Jika kita menemukan bukti yang cukup untuk menolak hipotesis nol, maka kita menerima hipotesis alternatif.
- Angka Keyakinan (Confidence Value). Angka keyakinan atau confidence value adalah tingkat kepercayaan yang kita miliki terhadap hasil pengujian hipotesis. Biasanya, angka keyakinan dinyatakan dalam persentase, seperti 95% atau 99%. Semakin tinggi angka keyakinan, semakin kuat bukti yang diperoleh untuk menolak atau menerima hipotesis nol.
Contoh: Misalkan kita ingin menguji apakah pelatihan baru yang diberikan kepada karyawan perusahaan mampu meningkatkan produktivitas mereka. Dalam hal ini, hipotesis nol (H₀) akan menyatakan bahwa pelatihan baru tidak memiliki pengaruh terhadap produktivitas karyawan, sedangkan hipotesis alternatif (H₁) akan menyatakan bahwa pelatihan baru meningkatkan produktivitas karyawan.
Resiko Alpha dan Beta dalam Hipotesis Pembuktian Masalah
Nilai Alpha (α) dan Beta (β): Nilai alpha dan beta adalah kemungkinan kesalahan yang mungkin terjadi saat menolak atau menerima hipotesis nol.
Mari kita bahas mengenai risiko Alpha dan Beta dengan referensi yang Anda berikan dan memberikan contoh ilustrasi agar lebih mudah dipahami.
Risiko Alpha (α)
Risiko Alpha adalah risiko salah dalam menolak hipotesis nol (H₀). Jika tingkat kepercayaan yang dipilih adalah 95%, maka risiko Alpha adalah 5% atau 0,05.
Contoh: Ada kemungkinan 5% bahwa suatu produk dianggap cacat, padahal sebenarnya tidak cacat. Kita mengamati atau membuat keputusan bahwa ada perbedaan yang ada, padahal sebenarnya tidak ada perbedaan. Risiko Alpha juga disebut False Positive, Kesalahan Tipe I, atau “Risiko Produsen”.
Tingkat Kepercayaan = 1 – Risiko Alpha = 1 – α
Alpha disebut tingkat signifikansi dari suatu uji. Tingkat signifikansi umumnya antara 1% atau 10% tetapi dapat berupa nilai apa pun tergantung pada tingkat kepercayaan yang diinginkan atau kebutuhan untuk mengurangi kesalahan Tipe I. Jenis risiko ini hanya terjadi ketika H₀ ditolak.
Risiko Beta (β)
Risiko Beta adalah risiko bahwa keputusan akan dibuat bahwa produk tidak cacat ketika sebenarnya cacat. Dengan kata lain, ketika keputusan dibuat bahwa perbedaan tidak ada, padahal sebenarnya ada perbedaan. Jika kekuatan yang diinginkan adalah 90%, maka risiko Beta adalah 10%. Ada kemungkinan 10% bahwa keputusan akan dibuat bahwa produk tidak cacat, padahal sebenarnya cacat.
Berbeda dengan risiko Alpha, risiko Beta terjadi ketika H₀ tidak benar (atau ditolak).
Kekuatan (Power) = 1 – Risiko Beta = 1 – β
Risiko Beta juga disebut False Negative, Kesalahan Tipe II, atau “Risiko Konsumen”.
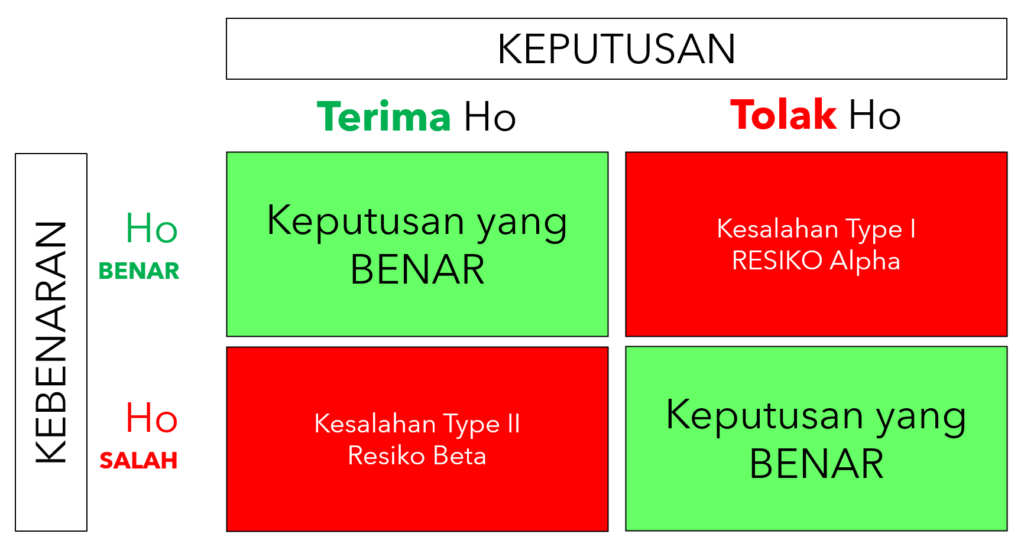
Kekuatan Hipotesis terhadap Alpha dan Beta
Kekuatan (Power) adalah kemungkinan untuk menolak hipotesis nol dengan benar.
Hipotesis nol secara teknis tidak pernah dibuktikan benar. Hipotesis ini “gagal untuk ditolak” atau “ditolak”.
Sebagai contoh, jika Anda melakukan uji F dan kesimpulan Anda adalah varians sama ketika sebenarnya tidak, itu akan mewakili kesalahan Tipe II. Biasanya, nilai ini ditetapkan antara 10-20%.
Sama seperti risiko Alpha, asumsi untuk risiko Beta harus disepakati dengan Black Belt/ Master Black Belt Anda.
Contoh: Risiko mengirim produk cacat yang sebenarnya cacat. “Konsumen” mengambil risiko karena Produsen membuat keputusan yang salah dan meletakkan produk buruk ini untuk Konsumen (atau pelanggan) gunakan atau beli, maka analogi mengapa risiko Beta juga dikenal sebagai “Risiko Konsumen”.
Risiko (atau kemungkinan) tidak menghukum (membebaskan) seseorang yang sebenarnya tidak bersalah.
Jenis Data dalam Analisis Statistik Six Sigma
Dalam analisis statistik Six Sigma, ada dua jenis data yang umumnya digunakan, yaitu data kategorikal (atau atribut) dan data kontinu:
- Data Kategorikal. Data kategorikal adalah data yang menggambarkan kategori atau atribut. Contoh data kategorikal adalah jenis produk yang dihasilkan, warna produk, atau departemen dalam suatu perusahaan. Data kategorikal biasanya dianalisis menggunakan metode statistik non-parametrik, seperti uji chi-square atau diagram Pareto.
- Data Kontinu. Data kontinu adalah data yang menggambarkan ukuran atau kuantitas, dan dapat memiliki nilai di antara dua titik di skala. Contoh data kontinu adalah waktu siklus produksi, biaya produksi, atau tingkat kecacatan produk. Data kontinu biasanya dianalisis menggunakan metode statistik parametrik, seperti uji-t, analisis varians (ANOVA), atau regresi linier.
Untuk memahami lebih baik, mari kita ambil contoh sebuah perusahaan yang ingin meningkatkan kualitas produk mereka. Perusahaan ini dapat mengumpulkan data kategorikal, seperti jenis produk yang dihasilkan dan departemen yang bertanggung jawab, serta data kontinu, seperti waktu siklus produksi dan jumlah produk cacat. Dengan menganalisis kedua jenis data ini secara terpadu, perusahaan dapat mengidentifikasi area yang memerlukan perbaikan dan mengambil tindakan yang tepat untuk meningkatkan kualitas produk mereka.
Untuk bahasan lebih dalam tentang jenis data dan Analisa statistic dalam Six Sigma akan saya bahas di artikel berikutnya ya?
Jadi, itulah pembahasan mengenai penggunaan alat statistik dalam metodologi Six Sigma, termasuk data, populasi, sampel, varians, deviasi, hipotesis, serta jenis data yang digunakan dalam analisis statistik. Semoga informasi ini bermanfaat dan memberikan Anda pemahaman yang lebih baik tentang bagaimana alat statistik digunakan dalam Six Sigma untuk mengidentifikasi dan mengurangi penyebab variasi dalam proses produksi atau layanan.
Selamat mencoba! Salam Produktivitas!
Dan Anda bisa terus belajar bersama dengan kami di Jago Kaizen dan Coach Wang.
Ingin mempelajari secara langsung dan privat Lean Six Sigma bersama Coach Wawang dalam membangun peningkatan kinerja dan eliminasi pemborosan?
PT Mitra Prima Produktivitas adalah provider coaching, mentoring, training, dan consulting ternama di Indonesia untuk kinerja Produktivitas dan peningkatan Profitabilitas.




